对于我们这样生活在三维空间的三维物种来说，要想象四维空间的样子是十分困难的。为了让你的三维大脑对四维空间产生一些模糊的感受，一个好办法就是让一位生活在二维空间中的扁片人来到三维空间，体验一下不同维度下的感受。我们不妨从这个角度开始分析吧。

A先生是一位生活在二维空间中的扁片人。我们邀请他参与回答这个问题的目的是为了分析三维人进入四维空间后的体验，所以我们假设A先生拥有和我们相似的能力。比如，虽然他的眼睛只能看见二维空间中的线条，但是他可以通过明暗、透视和双眼视差等方法感受二维物体的形状。这一切都由他的二维大脑完成。

当A先生观察这个正方形的时候，他的双眼看到的图像是不一样的。

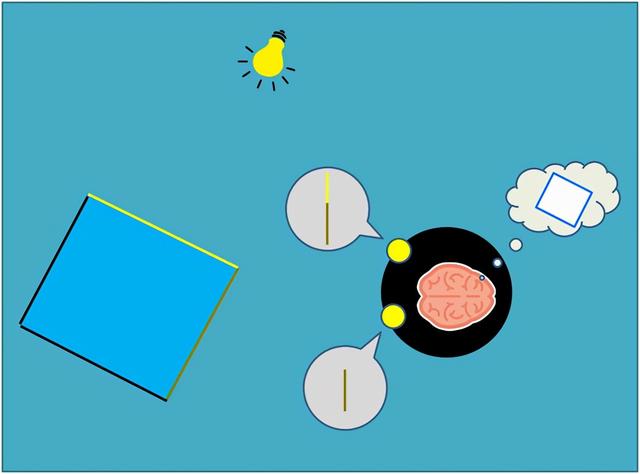
他的大脑可以把两个不同的图像组合起来，试图理解这个二维图形的形状。这个过程和三维人类大脑通过视网膜上的二维投影来理解三维世界是一样的。

现在，我们把A先生从二维空间中拎出来，放到三维空间中，并赋予他在三个维度上自由移动的能力。

虽然A先生来到了三维世界，但他仍然是一个二维的扁片人。他的一切生理结构，包括眼睛和大脑，都是为了适应二维世界而设计的。所以，他的眼睛还是只能看到点和线；他的大脑还只能识别二维图形。我们可以认为，A先生还是处于一个虚拟的二维空间中，只不过这个二维空间可以跟着他在三维空间中移动。

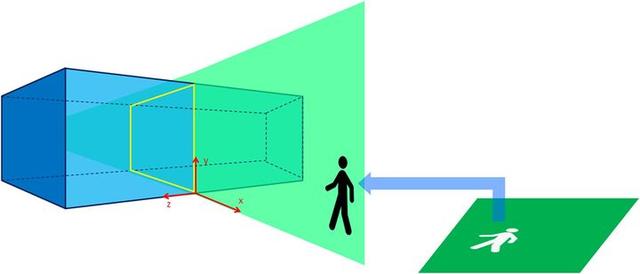
现在，A先生面对一个长方体。他看到的实际上是这个长方体和虚拟的二维平面相交的部分，也就是一个长方形。

如果A先生在第三维上移动，他会发现那个长方形也跟着他移动，而且大小和形状都不不变。如果A先生在三维空间中旋转，他会发现面前的长方形大小不断改变。这种情况无疑会使A先生和读者们感到十分无趣，所以，我们给他一个复杂一点的场景。

这次，A先生来的一个立方体面前，并且让他的虚拟二维平面和立方体的对角线EC垂直。

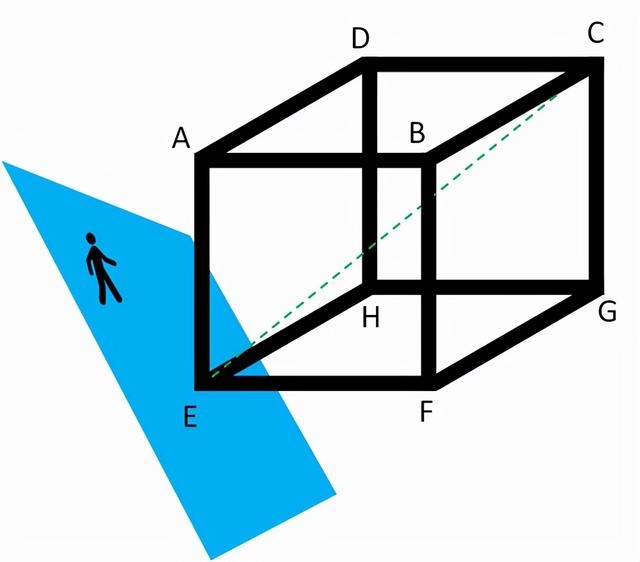
然后，A先生沿着对角线EC移动。在移动过程中，虚拟二维平面会和立方体的顶点相交。这时平面切割立方体形成的图形十分关键，它决定了在整个移动过程中，A先生会看到什么图形。

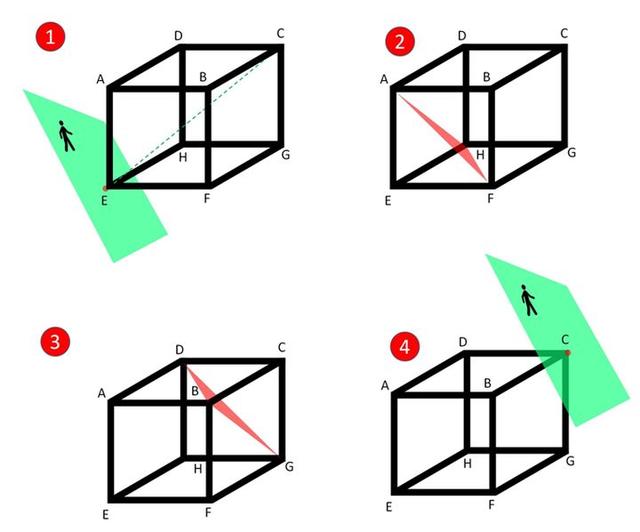
1. 首先，平面和E点相交。A先生会看到他的平面上出现一个点。然后，这个点扩展成一个三角形，并逐渐变大。

2. 当平面和顶点A、H、F相交时，A先生看到的图形是三角形AHF。

3. 当平面和顶点B、D、G相交时，A先生看到的是倒立的三角形BDG。

4. 最后，平面和顶点C相交。A先生看到的图形重新变成一个点。

5. 所以，在这4个瞬间，A先生看到的分别是以下4个图形。

而在这4个瞬间之间，图形会平滑变形，比如，从点变成三角形，从正放的三角形变成倒立的三角形。在两个三角形之间，过渡图形是逐渐变化的六边形。在上图中，我们只是列出了平面与立方体顶点相交时产生的图形。

闲话休提，书归正传，我们还是来看看你进入四维空间后，会看到什么情景吧。和A先生一样，虽然你进入了四维空间，但是你仍然是一个三维的人，无法看见四维物体。你也存在于一个虚拟的三维平面内，只能看见四维物体与这个平面相交形成的三维图形。

注：这里的“平面”是指比空间维度少一维的形状。在三维空间中，平面是二维的。在四维空间中，平面是三维的。我们不妨牵强附会地把它叫做三维平面吧。

要从上面的分析推导出四维空间的情形，我们需要一个简单的工具：帕斯卡三角_百度百科）。想必大多数人对这个名字都不会陌生。

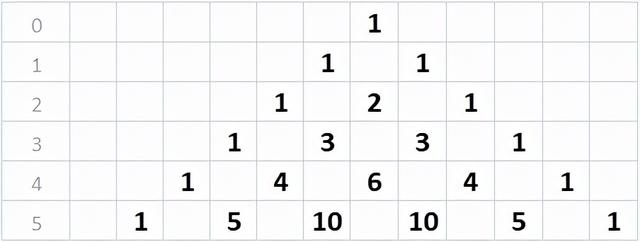
帕斯卡三角中隐藏了一个秘密：多维立方体被低维平面沿着对角线方向切割时，会产生什么图形？比如，我们上面对三维立方体进行了分析，得到了4个图形，它们的顶点数分别是1、3、3、1。这4个数字就藏在帕斯卡三角的第三行。

要想知道四维的超立方体被三维平面切割会产生什么图形，我们只需要看看帕斯卡三角的第四行。它包括5个数字：1、4、6、4、1。所以，在这个过程中，你会看到下面这些图形。

1. 首先，你会看到一个点。

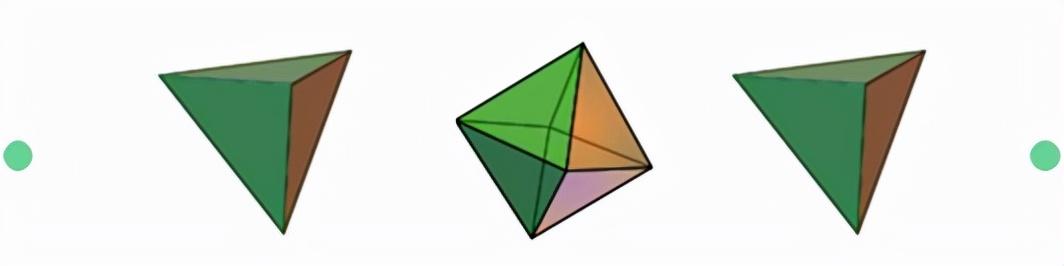
2. 这个点在三个维度上膨胀，变成一个4个顶点的三维图形：正四面体。

3. 然后，正四面体会逐渐变成一个6个顶点的三维图形：正八面体。

4. 下一步，正八面体会重新变形成为4个顶点的正四面体。

5. 最后，正四面体收缩成一个点，并最终消失。

也许你想挑战一下自己的空间想象能力，那么不妨看看帕斯卡三角的第五行，想象一下五维的超立方体被四维平面切割会是什么情景。

也许你会发现，一个超立方体穿越你的三维空间实际上是一样的。那么，我们还有什么必要亲自去四维空间走一趟。待在家里等着一个四维物体从我身边经过就行了。

其实，这两种情况还是有区别的。

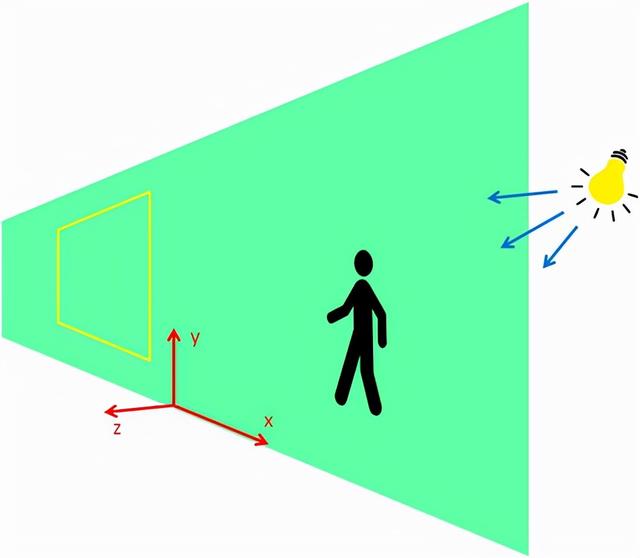
比如，A先生只能直接看到他的虚拟二维平面中的图形。然而，来自第三维度的光线也会从不同的方向进入这个平面，甚至直接落在他的视网膜上。对于身在四维空间中的你也同样如此。这些光绕过了晶状体，无法成像，所以你会看到一些难以名状光怪陆离的光影。

另外，如果你真的得到了一张体验四维空间的入场券，在启程之前请一定要三思，因为这实际上是一张通向地狱的门票。我们还是请扁片人A先生来做一个演示吧。

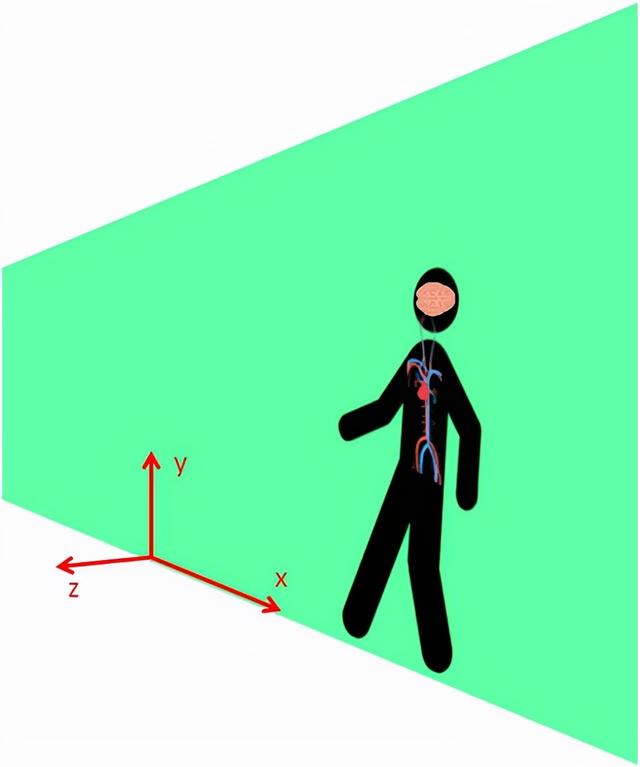
当A先生在他的二维家乡的时候，他所有的内脏都稳稳当当的安放在体内，没有任何危险。当他来到三维空间时，他的内部结构在第三维上完全暴露在外了。如果你进入四维空间，相同的事情也会发生在你身上。没有什么东西能够阻止你的内脏在第四维方向上掉出体外。由于内脏大多数是相互连接的，所以它们大概不会稀里哗啦滚落一地。不过它们晃晃悠悠地挂在体外的时候，应该无法执行它们正常的功能了。不要去细想这是一幅什么样的场景。我看过的恐怖片也没有一部能达到这个血腥程度。如果一个四维的智慧生物看到这一幕，估计够他做几天噩梦。

这还不算完。你体内的液体也会迅速从第四维方向流出来。而剩余的少量液体也会由于充分接触空气而很快蒸发掉。所以，你应该没有时间去欣赏四维空间的奇妙景象了。如果古埃及人发现了四维空间的秘密，估计会把它当成快速制作木乃伊的捷径。不过我们这样的三维凡夫俗子还是老老实实地坐在家里，期待有一天一个超立方体从眼前经过吧。